Bài Giảng Toán Cao Cấp

Xét không gian Euclide n chiều  \( {{\mathbb{R}}^{n}} \)  \( (n\ge 2) \) và tập hợp  \( D\subset {{\mathbb{R}}^{n}} \).

+ Một phần tử  \( x\in {{\mathbb{R}}^{n}} \) là một bộ n số thực  \( ({{x}_{1}},{{x}_{2}},…,{{x}_{n}})\,\,({{x}_{i}}\in \mathbb{R},\,\,i=1,…,n) \). Điểm M biểu diễn phần tử x trong  \( {{\mathbb{R}}^{n}} \) được gọi là có tọa độ  \( ({{x}_{1}},{{x}_{2}},…,{{x}_{n}}) \), kí hiệu  \( M({{x}_{1}},{{x}_{2}},…,{{x}_{n}}) \). Khoảng cách giữa  \( M({{x}_{1}},{{x}_{2}},…,{{x}_{n}}) \) và  \( N({{y}_{1}},{{y}_{2}},…,{{y}_{n}}) \) được kí hiệu và định nghĩa là

 \( d(M,N)=\sqrt{{{({{x}_{1}}-{{y}_{1}})}^{2}}+{{({{x}_{2}}-{{y}_{2}})}^{2}}+…+{{({{x}_{n}}-{{y}_{n}})}^{2}}} \).

+ Xét điểm  \( {{M}_{0}}\in {{\mathbb{R}}^{n}} \) và số thực  \( \varepsilon >0 \) bé tùy ý, ta gọi  \( \varepsilon  \) – lân cận (gọi tắt là lân cận) của điểm M₀ là tập hợp tất cả các điểm  \( M\in {{\mathbb{R}}^{n}} \) sao cho  \( d({{M}_{0}},M)<\varepsilon \) .

+ Điểm  \( M\in D \) được gọi là điểm trong của D nếu tồn tại một lân cận của điểm M nằm hoàn toàn trong D. Tập hợp D được gọi là tập mở nếu mọi điểm  \( M\in D \) đều là điểm trong của D.

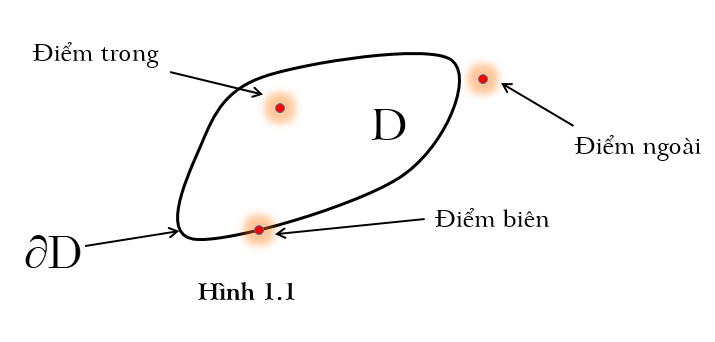
+ Điểm  \( M\in D \) được gọi là điểm biên của D nếu mọi lân cận của điểm M vừa chứa điểm thuộc D vừa chứa điểm không thuộc D (điểm biên của D có thể không thuộc D). Tập hợp tất cả các điểm biên của D được gọi là biên của D, kí hiệu là  \( \partial D \) (Xem hình 1.1). Tập hợp D được gọi là là tập đóng, kí hiệu là  \( \bar{D} \), nếu  \( \partial D\subset D \).

+ Xét điểm M₀ cố định và số thực  \( r>0 \). Tập hợp tất cả các điểm M sao cho  \( d({{M}_{0}},M)<r \) được gọi là quả cầu mở tâm M₀, bán kính r; tập hợp các điểm M thỏa  \( d({{M}_{0}},M)\le r \) được gọi là quả cầu đóng tâm M₀, bán kính r; tập hợp các điểm M thỏa  \( d({{M}_{0}},M)=r \) được gọi là mặt cầu tâm M₀, bán kính r. Tập hợp D được gọi là bị chặn nếu tồn tại một quả cầu đóng chứa D.

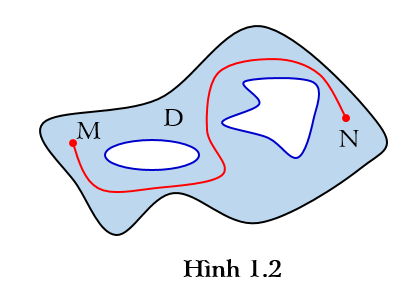
+ Tập D được gọi là tập liên thông nếu ta có thể nối hai điểm bất kì thuộc D bởi một đường cong liền nét nằm hoàn toàn trong D (Hình 1.2). Tập liên thông D được gọi là đơn liên nếu D có biên là một mặt cong kín (Hình 1.3); tập liên thông D có biên là hợp của nhiều mặt cong kín rời nhau được gọi là đa liên (Hình 1.4).