Bài Giảng Toán Cao Cấp
1.3. Giới hạn của hàm số hai biến
1. Định nghĩa 1.3.
Trong mặt phẳng Oxy, điểm \( {{M}_{0}}({{x}_{0}},{{y}_{0}}) \) được gọi là điểm tụ của dãy điểm \( {{\left\{ {{M}_{n}}({{x}_{n}},{{y}_{n}}) \right\}}_{n\in {{\mathbb{Z}}^{+}}}} \) nếu mọi lân cận của điểm \( {{M}_{0}}({{x}_{0}},{{y}_{0}}) \) đều chứa vô số phần tử của dãy.
+ Điểm O(0,0) là điểm tụ của dãy điểm \( {{\left\{ {{M}_{n}}\left( \frac{1}{n},\frac{1}{{{n}^{2}}} \right) \right\}}_{n\in {{\mathbb{Z}}^{+}}}} \).
+ Dãy điểm \( {{\left\{ {{M}_{n}}\left( \frac{1}{n},\sin n\frac{\pi }{2} \right) \right\}}_{n\in {{\mathbb{Z}}^{+}}}} \) có 3 điểm tụ là: \( O(0,0),\,\,A(0,-1) \) và \( B(0,1) \).
Nhận Dạy Kèm môn Giải Tích 2 - Calculus II Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Toán Cao Cấp gồm:
- Giải Tích 1, Giải Tích 2, Giải tích 3
- Đại Số Tuyến Tính, Xác Suất Thống Kê
- Sách Giải Bài Tập của bộ môn Toán Cao Cấp!
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học 1,5h - 2h/1 buổi!
2. Định nghĩa 1.4.
Điểm \( {{M}_{0}}({{x}_{0}},{{y}_{0}}) \) được gọi là giới hạn của dãy điểm \( {{\left\{ {{M}_{n}}({{x}_{n}},{{y}_{n}}) \right\}}_{n\in {{\mathbb{Z}}^{+}}}} \) nếu \( {{M}_{0}}({{x}_{0}},{{y}_{0}}) \) là điểm tụ duy nhất của dãy, kí hiệu là:
\( \underset{x\to \infty }{\mathop{\lim }}\,{{M}_{n}}={{M}_{0}} \) hay \( {{M}_{n}}\xrightarrow{n\to \infty }{{M}_{0}} \) hay \( {{M}_{n}}\to {{M}_{0}} \).
Vậy ta có \( {{M}_{n}}\to {{M}_{0}}\Leftrightarrow \underset{x\to \infty }{\mathop{\lim }}\,d({{M}_{n}},{{M}_{0}})=0 \).
+ Giả sử hàm số \( z=f(x,y) \) xác định trong một lân cận V nào đó của điểm \( {{M}_{0}}({{x}_{0}},{{y}_{0}}) \) (có thể trừ điểm \( {{M}_{0}} \)). Ta nói hàm f có giới hạn là L khi \( M(x,y)\to {{M}_{0}} \) nếu mọi dãy điểm \( {{\left\{ {{M}_{n}}({{x}_{n}},{{y}_{n}}) \right\}}_{n\in {{\mathbb{Z}}^{+}}}} \) thuộc \(V\backslash \{{{M}_{0}}\}\) dần đến \( {{M}_{0}} \) ta đều có \(\underset{n\to \infty }{\mathop{\lim }}\,f({{x}_{n}},{{y}_{n}})=L\), kí hiệu là:
\( \underset{(x,y)\to ({{x}_{0}},{{y}_{0}})}{\mathop{\lim }}\,f(x,y)=L \) hay \( \underset{\begin{smallmatrix} x\to {{x}_{0}} \\ y\to {{y}_{0}} \end{smallmatrix}}{\mathop{\lim }}\,f(x,y)=L \) hay \( \underset{M\to {{M}_{0}}}{\mathop{\lim }}\,f(M)=L \).
Chú ý:
– Định nghĩa trên có thể phân biệt cách khác tương đương như sau: Hàm số f(M) có giới hạn là L (Hình 1.6) Khi \( M\to {{M}_{0}} \) nếu \( \forall \varepsilon >0,\,\,\exists \delta >0,\forall M\in {{D}_{f}}:0<d(M,{{M}_{0}})<\delta \Rightarrow \left| f(M)-L \right|<\varepsilon \).
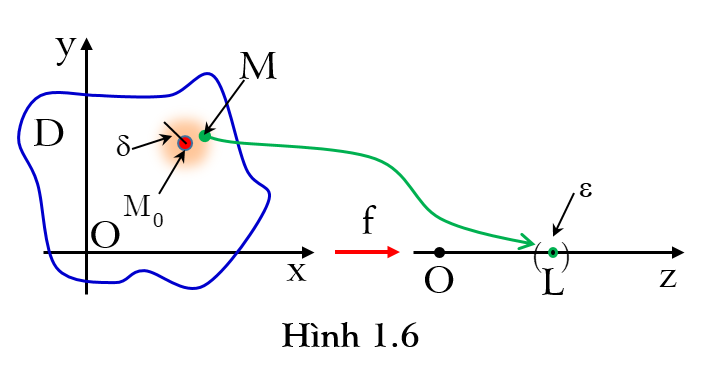
– Giới hạn (nếu có) là duy nhất.
– Khái niệm giới hạn vô cùng; các định lí về giới hạn của tổng, tích, thương được định nghĩa tương tự như đối với hàm số một biến.
Ví dụ 1. \( \underset{(x,y)\to (0,\pi )}{\mathop{\lim }}\,\cos (x{{y}^{2}}-y)=-1 \).
Ví dụ 2. \( \underset{(x,y)\to (-\infty ,+\infty )}{\mathop{\lim }}\,\frac{1}{\sqrt{{{x}^{2}}+{{y}^{2}}}}=0 \).
Ví dụ 3. Tìm \( \underset{(x,y)\to (0,0)}{\mathop{\lim }}\,f(x,y) \), với \( f(x,y)=\frac{xy}{\sqrt{{{x}^{2}}+{{y}^{2}}}} \).
Hướng dẫn giải:
Khi \( (x,y)\to (0,0) \) thì \( (x,y)\ne (0,0) \), ta có:
\( 0\le \frac{{{y}^{2}}}{{{x}^{2}}+{{y}^{2}}}\le 1\Rightarrow 0\le \frac{\left| y \right|}{\sqrt{{{x}^{2}}+{{y}^{2}}}}\le 1 \) hay \( 0\le \left| f(x,y) \right|\frac{\left| y \right|}{\sqrt{{{x}^{2}}+{{y}^{2}}}}\left| x \right|\le \left| x \right| \)
Suy ra \( 0\le \underset{(x,y)\to (0,0)}{\mathop{\lim }}\,f(x,y)\le \underset{(x,y)\to (0,0)}{\mathop{\lim }}\,\left| x \right|=0 \).
Áp dụng định lí giới hạn kẹp giữa, ta được \( \underset{(x,y)\to (0,0)}{\mathop{\lim }}\,f(x,y)=0 \).
Nhận xét: Nếu đặt \( x={{x}_{0}}+r\cos \varphi \) và \( y={{y}_{0}}+r\sin \varphi \) thì ta có:
\( (x,y)\to ({{x}_{0}},{{y}_{0}})\Leftrightarrow r\to 0 \)
Ví dụ 4. Tìm \( \underset{(x,y)\to (0,0)}{\mathop{\lim }}\,\frac{\sin ({{x}^{2}}+{{y}^{2}})}{{{x}^{2}}+{{y}^{2}}} \).
Hướng dẫn giải:
Đặt \( x=r\cos \varphi \) và \( y=r\sin \varphi \), ta có:
\( \underset{(x,y)\to (0,0)}{\mathop{\lim }}\,\frac{\sin ({{x}^{2}}+{{y}^{2}})}{{{x}^{2}}+{{y}^{2}}}=\underset{r\to 0}{\mathop{\lim }}\,\frac{\sin {{r}^{2}}}{{{r}^{2}}}=1 \).
Ví dụ 5. Cho hàm số \( f(x,y)=\frac{2xy}{{{x}^{2}}+{{y}^{2}}} \). Chứng tỏ rằng \( \underset{(x,y)\to (0,0)}{\mathop{\lim }}\,f(x,y) \) không tồn tại.
Hướng dẫn giải:
Đặt \( x=r\cos \varphi \) và \( y=r\sin \varphi \) , ta có:
\( \underset{(x,y)\to (0,0)}{\mathop{\lim }}\,f(x,y)=\underset{r\to 0}{\mathop{\lim }}\,\frac{{{r}^{2}}\sin 2\varphi }{{{r}^{2}}}=\sin 2\varphi \).
Do giới hạn phụ thuộc vào \( \varphi \) nên không duy nhất.
Vậy \( \underset{(x,y)\to (0,0)}{\mathop{\lim }}\,f(x,y) \) không tồn tại.
Cách khác:
– Cho điểm \( M(x,y)\to O(0,0) \) trên đường thẳng \( y=x \), ta được:
\( \underset{(x,y)\to (0,0)}{\mathop{\lim }}\,f(x,y)=\underset{(x,y)\to (0,0)}{\mathop{\lim }}\,\frac{2{{x}^{2}}}{{{x}^{2}}+{{x}^{2}}}=1 \)
– Cho điểm \( M(x,y)\to O(0,0) \) trên đường thẳng \( y=-x \), ta được:
\( \underset{(x,y)\to (0,0)}{\mathop{\lim }}\,f(x,y)=\underset{(x,y)\to (0,0)}{\mathop{\lim }}\,\frac{-2{{x}^{2}}}{{{x}^{2}}+{{x}^{2}}}=-1 \)
Do khi \( M(x,y)\to O(0,0) \) theo các đường khác nhau thì giới hạn khác nhau nên không tồn tại \( \underset{(x,y)\to (0,0)}{\mathop{\lim }}\,f(x,y) \).
3. Giới hạn lặp.
+ Định nghĩa 1.5. Giới hạn theo từng biến khi \( M(x,y)\to {{M}_{0}}({{x}_{0}},{{y}_{0}}) \) của hàm số \( f(x,y) \) được gọi là giới hạn lặp.
+ Khi \( x\to {{x}_{0}} \) trước và \( y\to {{y}_{0}} \) sau thì ta viết \(\underset{y\to {{y}_{0}}}{\mathop{\lim }}\,\left[ \underset{x\to {{x}_{0}}}{\mathop{\lim }}\,f(x,y) \right]=\underset{y\to {{y}_{0}}}{\mathop{\lim }}\,\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,f(x,y)\)
+ Khi \( y\to {{y}_{0}} \) trước và \( x\to {{x}_{0}} \) sau thì ta viết \(\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\left[ \underset{y\to {{y}_{0}}}{\mathop{\lim }}\,f(x,y) \right]=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\underset{y\to {{y}_{0}}}{\mathop{\lim }}\,f(x,y)\)
+ Chú ý 1.3:
– Nếu \(\underset{y\to {{y}_{0}}}{\mathop{\lim }}\,\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,f(x,y)\ne \underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\underset{y\to {{y}_{0}}}{\mathop{\lim }}\,f(x,y)\) thì \( \cancel{\exists }\underset{(x,y)\to ({{x}_{0}},{{y}_{0}})}{\mathop{\lim }}\,f(x,y) \).
– Nếu \(\underset{y\to {{y}_{0}}}{\mathop{\lim }}\,\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,f(x,y)=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\underset{y\to {{y}_{0}}}{\mathop{\lim }}\,f(x,y)\) thì ta chưa thể kết luận được có tồn tại \( \underset{(x,y)\to ({{x}_{0}},{{y}_{0}})}{\mathop{\lim }}\,f(x,y) \) hay không.
Ví dụ 6. Cho hàm số \( f(x,y)=\frac{\sin {{x}^{2}}-\sin {{y}^{2}}}{{{x}^{2}}+{{y}^{2}}} \). Chứng tỏ rằng \( \underset{(x,y)\to ({{x}_{0}},{{y}_{0}})}{\mathop{\lim }}\,f(x,y) \) không tồn tại.
Hướng dẫn giải:
Ta có: \(\underset{y\to 0}{\mathop{\lim }}\,\underset{x\to 0}{\mathop{\lim }}\,f(x,y)=\underset{y\to 0}{\mathop{\lim }}\,\frac{-\sin {{y}^{2}}}{{{y}^{2}}}=-1\).
\(\underset{x\to 0}{\mathop{\lim }}\,\underset{y\to 0}{\mathop{\lim }}\,f(x,y)=\underset{x\to 0}{\mathop{\lim }}\,\frac{\sin {{x}^{2}}}{{{x}^{2}}}=1\).
Do \(\underset{y\to 0}{\mathop{\lim }}\,\underset{x\to 0}{\mathop{\lim }}\,f(x,y)\ne \underset{x\to 0}{\mathop{\lim }}\,\underset{y\to 0}{\mathop{\lim }}\,f(x,y)\) nên \( \cancel{\exists }\underset{(x,y)\to (0,0)}{\mathop{\lim }}\,f(x,y) \).
