Bài Giảng Toán Cao Cấp
2.5. Đạo hàm theo hướng – Vectơ gradient
1. Hàm vectơ
+ Định nghĩa 1.14.
– Ánh xạ \( \vec{r}:T\subset \mathbb{R}\to {{\mathbb{R}}^{n}} \)
\( t\mapsto \vec{r}(t)=\left( {{x}_{1}}(t),{{x}_{2}}(t),…,{{x}_{n}}(t) \right) \) được gọi là một hàm vectơ.
– Đạo hàm của hàm vectơ được xác định:
\({\vec{r}}'(t)=\underset{t\to {{t}_{0}}}{\mathop{\lim }}\,\frac{\vec{r}(t)-\vec{r}({{t}_{0}})}{t-{{t}_{0}}}=\underset{t\to {{t}_{0}}}{\mathop{\lim }}\,\left( \frac{{{x}_{1}}(t)-{{x}_{1}}({{t}_{0}})}{t-{{t}_{0}}},…,\frac{{{x}_{n}}(t)-{{x}_{n}}({{t}_{0}})}{t-{{t}_{0}}} \right)\).
Vậy ta có công thức tính đạo hàm của hàm vectơ là: \( {\vec{r}}'(t)=\left( {{{{x}’}}_{1}}(t),{{{{x}’}}_{2}}(t),…,{{{{x}’}}_{n}}(t) \right) \).
– Trong \( {{\mathbb{R}}^{n}} \), ta đặt \( \vec{r}(t)=\overrightarrow{OM} \). Khi t thay đổi thì điểm M thay đổi và vạch ra một đường cong. Đường cong này được gọi là tốc đồ của \( \vec{r}(t) \). Phương trình tham số của tốc đồ là:
\( {{x}_{1}}={{x}_{1}}(t),\,\,{{x}_{2}}={{x}_{2}}(t),…,\,\,{{x}_{n}}={{x}_{n}}(t) \).
+ Chú ý 1.8:
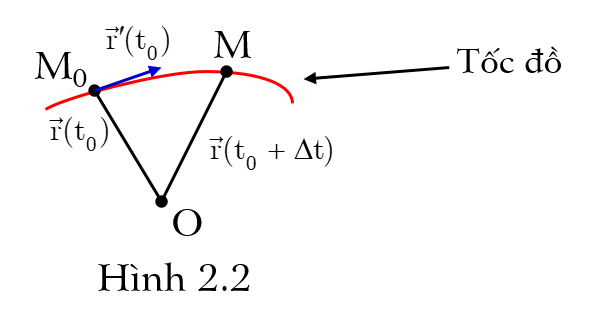
– Tại điểm M0 thuộc tốc đồ của \( \vec{r}(t) \), nếu \( {\vec{r}}'({{t}_{0}}) \) khác \( \vec{0} \) thì \( {\vec{r}}'({{t}_{0}}) \) là vectơ chỉ phương tiếp tuyến tại điểm M0 của tốc đồ (Hình 2.2).
– Nếu \( {\vec{r}}'({{t}_{0}})=\vec{0} \) thì điểm M0 được gọi là điểm kỳ dị của tốc đồ.
Nhận Dạy Kèm môn Giải Tích 2 - Calculus II Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Toán Cao Cấp gồm:
- Giải Tích 1, Giải Tích 2, Giải tích 3
- Đại Số Tuyến Tính, Xác Suất Thống Kê
- Sách Giải Bài Tập của bộ môn Toán Cao Cấp!
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học 1,5h - 2h/1 buổi!
2. Đạo hàm theo hướng
+ Định nghĩa 1.15.
– Giả sử hàm số \( f(M) \) xác định trong lân cận V của điểm \( {{M}_{0}}\in {{\mathbb{R}}^{n}} \). Xét \( \vec{v}\ne \vec{0} \), gọi \( \Delta \) là nửa đường thẳng gốc M0 theo hướng \( \vec{v} \). Trên \( \Delta \) , ta lấy điểm M sao cho đoạn \( {{M}_{0}}M \) thuộc V và đặt \( r={{M}_{0}}M \). Đạo hàm tại điểm M0 theo hướng \( \vec{v} \) của hàm \( f(M) \), kí hiệu \( {{{f}’}_{{\vec{v}}}}({{M}_{0}}) \), là giới hạn (nếu có) của tỉ số \( \frac{f(M)-f({{M}_{0}})}{r} \) khi \( r\to 0 \).
Vậy \({{{f}’}_{{\vec{v}}}}({{M}_{0}})=\underset{r\to 0}{\mathop{\lim }}\,\frac{f(M)-f({{M}_{0}})}{r}\)
– Trong mặt phẳng tọa độ Oxy, gọi \( \alpha ,\beta \) lần lượt là góc tạo bởi \( \vec{v}=({{v}_{x}},{{v}_{y}}) \) (khác \( \vec{0} \)) với \( \overrightarrow{i} \) và \( \overrightarrow{j} \). Khi đó \( \cos \alpha ,\,\,\cos \beta \) được gọi là các cosin chỉ phương của \( \vec{v} \) và
\( \cos \alpha =\frac{{{v}_{x}}}{\left| {\vec{v}} \right|},\,\,\cos \beta =\frac{{{v}_{y}}}{\left| {\vec{v}} \right|} \)
– Trong Oxyz, gọi \(\alpha ,\beta ,\gamma \) lần lượt là góc tạo bởi \( \vec{v}=({{v}_{x}},{{v}_{y}},{{v}_{z}}) \) (khác \( \vec{0} \)) với \( \overrightarrow{i},\overrightarrow{j},\vec{k} \). Khi đó \( \cos \alpha ,\,\,\cos \beta \) và \( \cos \gamma \) được gọi là các cosin chỉ phương của \( \vec{v} \) và
\( \cos \alpha =\frac{{{v}_{x}}}{\left| {\vec{v}} \right|},\,\,\cos \beta =\frac{{{v}_{y}}}{\left| {\vec{v}} \right|},\,\,\cos \gamma =\frac{{{v}_{z}}}{\left| {\vec{v}} \right|} \).
+ Định nghĩa 1.5
– Nếu hàm số \( f(x,y) \) khả vi tại điểm \( {{M}_{0}}\in {{\mathbb{R}}^{2}} \) thì tồn tại đạo hàm tại điểm \( {{M}_{0}} \) theo hướng \( \vec{v}\ne \vec{0} \) bất kì và
\( {{{f}’}_{{\vec{v}}}}({{M}_{0}})={{{f}’}_{x}}({{M}_{0}})\cos \alpha +{{{f}’}_{y}}({{M}_{0}})\cos \beta \)
– Nếu hàm số \( f(x,y,z) \) khả vi tại điểm \( {{M}_{0}}\in {{\mathbb{R}}^{3}} \) thì tồn tại đạo hàm tại điểm M0 theo hướng \( \vec{v}\ne \vec{0} \) bất kì và
\( {{{f}’}_{{\vec{v}}}}({{M}_{0}})={{{f}’}_{x}}({{M}_{0}})\cos \alpha +{{{f}’}_{y}}({{M}_{0}})\cos \beta +{{{f}’}_{z}}({{M}_{0}})\cos \gamma \)
+ Hệ quả 1.1
Đạo hàm theo hướng các vectơ chỉ phương của các trục tọa độ của hàm số \( f(x,y,z) \) tại điểm \( {{M}_{0}}\in {{\mathbb{R}}^{3}} \) là
\( {{{f}’}_{\overrightarrow{i}}}({{M}_{0}})={{{f}’}_{x}}({{M}_{0}}),\,\,{{{f}’}_{\overrightarrow{j}}}({{M}_{0}})={{{f}’}_{y}}({{M}_{0}}),\,\,{{{f}’}_{\overrightarrow{k}}}({{M}_{0}})={{{f}’}_{z}}({{M}_{0}}) \)
3. Vectơ gradient
+ Định nghĩa 1.16
– Giả sử hàm số \( f(x,y) \) có các đạo hàm riêng tại điểm \( {{M}_{0}}\in {{\mathbb{R}}^{2}} \). Vectơ gradient tại điểm M0 của hàm số \( f(x,y) \), kí hiệu \( \nabla f({{M}_{0}}) \) hay \( \overrightarrow{grad}f({{M}_{0}}) \), là vectơ
\( \nabla f({{M}_{0}})={{{f}’}_{x}}({{M}_{0}})\cdot \overrightarrow{i}+{{{f}’}_{y}}({{M}_{0}})\cdot \overrightarrow{j}=\left( {{{{f}’}}_{x}}({{M}_{0}}),{{{{f}’}}_{y}}({{M}_{0}}) \right) \)
– Tương tự, hàm \( f(x,y,z) \) có các đạo hàm riêng tại điểm M0 thì
\( \nabla f({{M}_{0}})={{{f}’}_{x}}({{M}_{0}})\cdot \overrightarrow{i}+{{{f}’}_{y}}({{M}_{0}})\cdot \overrightarrow{j}+{{{f}’}_{z}}({{M}_{0}})\cdot \vec{k}=\left( {{{{f}’}}_{x}}({{M}_{0}}),{{{{f}’}}_{y}}({{M}_{0}}),{{{{f}’}}_{z}}({{M}_{0}}) \right) \)
+ Ý nghĩa hình học của vectơ gradient
– Trong mặt phẳng tọa độ Oxy, xét đường cong \( (C):f(x,y)=0 \). Giả sử (C) có tiếp tuyến tại \( {{M}_{0}}\in (C) \) là \( \Delta \) , khi đó vectơ pháp tuyến \( \Delta \) là \( {{\vec{n}}_{\Delta }}=\nabla f({{M}_{0}}) \) (Hình 2.3)
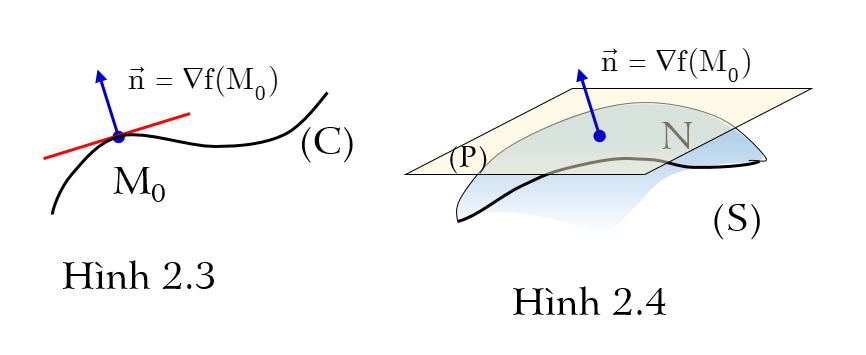
– Trong không gian Oxyz, xét mặt cong \( (S):f(x,y,z)=0 \). Giả sử (S) có tiếp diện tại \( {{M}_{0}}\in (S) \) là (P), khi đó vectơ pháp tuyến của tiếp diện (P) là \( {{\vec{n}}_{P}}=\nabla f({{M}_{0}}) \) (Hình 2.4)
Ví dụ 1. Cho hàm \( f(x,y,z)=\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}} \) và \( \vec{v}=(1,-2,-2) \). Tính \( {{{f}’}_{{\vec{v}}}}(M) \) và \( \nabla f(M) \) tại điểm \( M(0,4,-3) \).
Hướng dẫn giải:
Ta có: \( {{{f}’}_{x}}=\frac{x}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}},\,\,{{{f}’}_{y}}=\frac{y}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}},\,\,{{{f}’}_{z}}=\frac{z}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}} \).
Suy ra: \( {{{f}’}_{x}}(M)=0,\,\,{{{f}’}_{y}}(M)=\frac{4}{5},\,\,{{{f}’}_{z}}(M)=-\frac{3}{5} \).
Mặt khác: \( \cos \alpha =\frac{1}{3},\,\,\cos \beta =-\frac{2}{3},\,\,\cos \gamma =-\frac{2}{3} \).
Vậy, ta có: \( {{{f}’}_{{\vec{v}}}}(M)=0\cdot \frac{1}{3}+\frac{4}{5}\cdot \frac{-2}{3}+\frac{-3}{5}\cdot \frac{-2}{3}=-\frac{2}{15} \) và \( \nabla f(M)=\left( 0,\frac{4}{5},-\frac{3}{5} \right) \).
Sách Giải Bài Tập Giải Tích 2
Ví dụ 2. Trong mặt phẳng, cho đường cong \( (C):{{x}^{2}}-{{y}^{2}}-3xy+2y-1=0 \). Viết phương trình tiếp tuyến \( \Delta \) với (C) tại điểm \( M(1,-1) \).
Hướng dẫn giải:
Ta có: \( f(x,y)={{x}^{2}}-{{y}^{2}}-3xy+2y-1 \), suy ra:
\( \left\{ \begin{align} & {{{{f}’}}_{x}}(x,y)=2x-3y \\ & {{{{f}’}}_{y}}(x,y)=-2y-3x+2 \\ \end{align} \right. \) \( \Rightarrow \left\{ \begin{align} & {{{{f}’}}_{x}}(M)=5 \\ & {{{{f}’}}_{y}}(M)=1 \\ \end{align} \right.\Rightarrow {{\vec{n}}_{\Delta }}=(5,1) \).
Vậy \( \Delta :5x+y-4=0 \).
Ví dụ 3. Trong không gian, cho mặt parabolic eliptic \( (S):z=\frac{{{x}^{2}}}{4}+{{y}^{2}}-2 \). Viết phương trình tiếp diện (P) với (S) tại điểm \( M(2,-3,8) \).
Hướng dẫn giải:
Ta có \( (S):{{x}^{2}}+4{{y}^{2}}-4z-8=0 \) nên \( f(x,y,z)={{x}^{2}}+4{{y}^{2}}-4z-8 \).
Từ \( \left\{ \begin{align} & {{{{f}’}}_{x}}(M)=4 \\ & {{{{f}’}}_{y}}(M)=-24 \\ & {{{{f}’}}_{z}}(M)=-4 \\ \end{align} \right. \) ta suy ra \( {{\vec{n}}_{P}}=(1,-6,-1) \).
Vậy \( (P):x-6y-z-12=0 \).
