Bài Giảng Toán Cao Cấp
2.4.3. Công thức tính tích phân bội ba trong tọa độ cầu
a) Tọa độ cầu
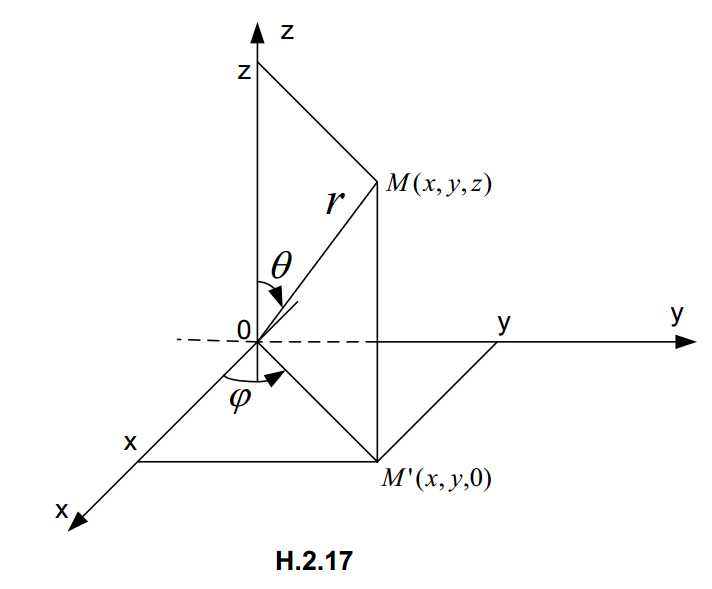
Tọa độ cầu của một điểm \( M(x,y,z)\in Oxyz \) là bộ ba số \( (r,\theta ,\varphi ) \) trong đó \( r=\left| \overrightarrow{OM} \right|,\,\,\theta \) là góc giữa trục Oz và \(\overrightarrow{OM} \), \( \varphi \) là góc giữa trục Ox và \( \overrightarrow{OM’} \), ở đây M’ là hình chiếu của M trên Oxy (H.2.17). Vậy với mọi điểm của không gian sẽ có: \( r\ge 0,\,\,0\le \theta \le \pi ,\,\,0\le \varphi <2\pi \) . Dễ thấy giữa các tọa độ Descartes và tọa độ cầu có mối quan hệ: \( \left\{ \begin{align} & x=r\sin \theta \cos \varphi \\ & y=r\sin \theta \sin \varphi \\ & z=r\cos \theta \\ \end{align} \right. \).
Và như vậy \( \frac{D(x,y,z)}{D(r,\theta ,\varphi )}=\left| \begin{matrix} \sin \theta \cos \varphi & r\cos \theta \cos \varphi & -\sin \theta \sin \varphi \\ \sin \theta \sin \varphi & r\cos \theta \cos \varphi & r\sin \theta \cos \varphi \\ \cos \theta & -r\sin \theta & 0 \\\end{matrix} \right|=-{{r}^{2}}\sin \theta \,\,\,\,\,\,\,(2.24) \)
Nhận Dạy Kèm môn Giải Tích 2 - Calculus II Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Toán Cao Cấp gồm:
- Giải Tích 1, Giải Tích 2, Giải tích 3
- Đại Số Tuyến Tính, Xác Suất Thống Kê
- Sách Giải Bài Tập của bộ môn Toán Cao Cấp!
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học 1,5h - 2h/1 buổi!
b) Phương trình mặt cong trong tọa độ cầu
Hệ thức \( F(r,\theta ,\varphi )=0 \) hoặc giải ra được đối với các biến số \( r=r(\theta ,\varphi );\,\,\theta =\theta (\varphi ,r);\,\,\varphi =\varphi (r,\theta ) \) gọi là một phương trình mặt cong trong tọa độ cầu. Các trường hợp đặc biệt thường gặp sau đây:
+ \( r={{r}_{0}} \) mô tả mặt cầu tâm gốc tọa độ O và bán kính \( {{r}_{0}} \) (trong hệ tọa độ Oxyz, mặt cầu này có phương trình \( {{x}^{2}}+{{y}^{2}}+{{z}^{2}}=r_{0}^{2} \)).
+ \( \theta ={{\theta }_{0}} \) là phương trình của mặt nón tròn xoay, đỉnh O và trục đối xứng là Oz có góc mở là \( 2\theta \) (mặt nón này trong hệ Oxyz có phương trình \( \sqrt{{{x}^{2}}+{{y}^{2}}}=\tan \theta \cdot z \)).
+ \( \varphi ={{\varphi }_{0}} \) là phương trình nửa mặt phẳng lập với mặt phẳng Oxy một góc \( {{\varphi }_{0}} \) (nửa mặt phẳng này trong hệ tọa độ Oxyz có phương trình \( y=\tan {{\varphi }_{0}}\cdot x \) với \( x\cos {{\varphi }_{0}}\ge 0 \)).
c) Công thức tính tích phân bội ba trong tọa độ cầu
Từ công thức (2.20) và (2.24) ta nhận được:
\(\iiint\limits_{V}{f(x,y,z)dxdydz}=\iiint\limits_{\Omega }{f(r\sin \theta \cos \varphi ,r\sin \theta \sin \varphi ,r\cos \theta ){{r}^{2}}\sin \theta drd\theta d\varphi }\,\,\,\,\,\,(2.25)\)
Ta hay gặp miền \( \Omega \) trong tọa độ cầu mô tả bởi hệ bất phương trình: \( \left\{ \begin{align} & {{\varphi }_{1}}\le \varphi \le {{\varphi }_{2}} \\ & {{\theta }_{1}}(\varphi )\le \theta \le {{\theta }_{2}}(\varphi ) \\ & {{r}_{2}}(\theta ,\varphi )<r\le {{r}_{2}}(\theta ,\varphi ) \\ \end{align} \right. \).
Khi đó công thức (2.25) trở thành:
\(\iiint\limits_{V}{f(x,y,z)dxdydz}=\int\limits_{{{\varphi }_{1}}}^{{{\varphi }_{2}}}{d\varphi }\int\limits_{{{\theta }_{1}}(\varphi )}^{{{\theta }_{2}}(\varphi )}{\sin \theta d\theta }\int\limits_{{{r}_{1}}(\theta ,\varphi )}^{{{r}_{2}}(\theta ,\varphi )}{f(r\sin \theta \cos \varphi ,r\sin \theta \sin \varphi ,r\cos \theta ){{r}^{2}}dr}\,\,\,\,\,\,(2.26)\)
Sách Giải Bài Tập Giải Tích 2
Ví dụ 1. Tính \( I=\iiint\limits_{V}{\frac{1}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}}dxdydz} \), trong đó V là miền giới hạn bởi hai mặt cầu \( {{x}^{2}}+{{y}^{2}}+{{z}^{2}}=1 \) và \( {{x}^{2}}+{{y}^{2}}+{{z}^{2}}=4 \).
Hướng dẫn giải:
Chuyển sang tọa độ cầu, hai mặt cầu đã cho có phương trình lần lượt là \( r=1,\,\,r=2 \). Gốc tọa độ là điểm trong của miền V nên miền \( \Omega \) cho bởi hệ bất phương trình: \( \left\{ \begin{align} & 0\le \varphi \le 2\pi \\ & 0\le \theta \le \pi \\ & 1\le r\le 2 \\ \end{align} \right. \).
Do đó: \( I=\int\limits_{0}^{2\pi }{d\varphi }\int\limits_{0}^{\pi }{\sin \theta d\theta }\int\limits_{1}^{2}{\frac{1}{r}\cdot {{r}^{2}}dr}=2\pi \left. (-\cos \theta ) \right|_{0}^{\pi }\cdot \left. \frac{1}{2}{{r}^{2}} \right|_{1}^{2}=6\pi \).
Ví dụ 2. Tính \(I=\iiint\limits_{V}{({{x}^{2}}+{{y}^{2}})dxdydz}\) trong đó V là miền ngoài giữa hình trụ \( {{x}^{2}}+{{y}^{2}}\le {{R}^{2}} \) và hình cầu \( {{x}^{2}}+{{y}^{2}}+{{z}^{2}}\le 4{{R}^{2}} \).
Hướng dẫn giải:
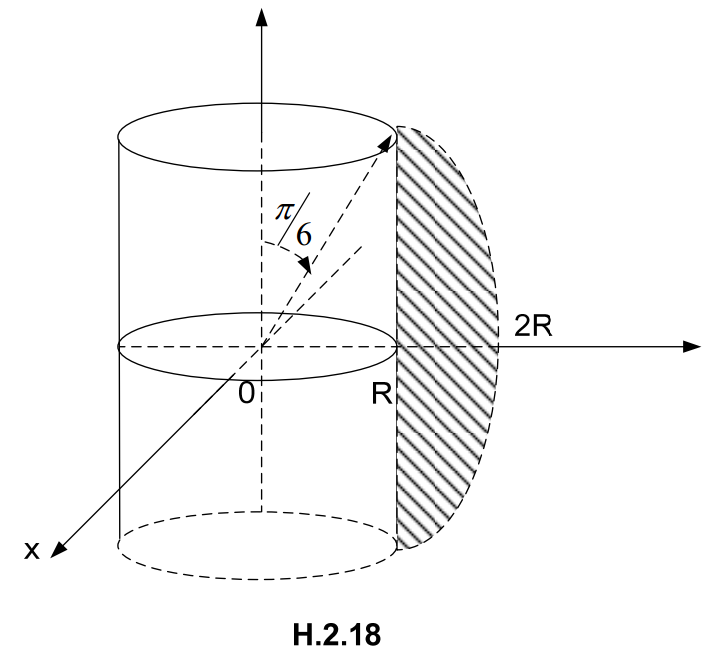
Một thiết diện của miền V cho trên hình H.2.18. Xét trong hệ tọa độ cầu, mặt cầu có phương trình \( r=2R \), mặt trụ có phương trình \( r=\frac{R}{\sin \theta } \) (thay \( x=r\sin \theta \cos \varphi ,\,\,y=r\sin \theta \sin \varphi \) vào phương trình \( {{x}^{2}}+{{y}^{2}}={{R}^{2}} \) sẽ nhận được kết quả trên). Để tìm sự biến thiên của \( \theta \) ta xét giao của mặt cầu và mặt trụ: \( r=2R=\frac{R}{\sin \theta } \).
Suy ra: \( \sin \theta =\frac{1}{2}\Rightarrow \theta =\frac{\pi }{6},\,\,\theta =\frac{5\pi }{6} \).
Vì V là vật thể tròn xoay nhận Oz làm trục đối xứng, nhận mặt phẳng Oxy làm mặt phẳng đối xứng và hàm dưới dấu tích phân chẵn đối với x, y cho nên
\( I=2\int\limits_{0}^{2\pi }{d\varphi }\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{2}}{\sin \theta d\theta }\int\limits_{\frac{R}{\sin \theta }}^{2R}{{{r}^{4}}{{\sin }^{2}}\theta dr}=\frac{4}{5}\pi {{R}^{5}}\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{2}}{\left( 32-\frac{1}{{{\sin }^{5}}\theta } \right){{\sin }^{3}}\theta d\theta } \)
\( =\frac{4}{5}\pi {{R}^{5}}\left[ 32\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{2}}{\sin \theta (1-{{\cos }^{2}}\theta )d\theta }-\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{2}}{\frac{1}{{{\sin }^{2}}\theta }d\theta } \right]=\frac{4}{5}\pi {{R}^{5}}\left. \left[ 32(-\cos \theta +\frac{1}{3}{{\cos }^{3}}\theta )+\cot \theta \right] \right|_{\frac{\pi }{6}}^{\frac{\pi }{2}}=\frac{44\sqrt{3}}{5}\pi {{R}^{5}} \).
Chú ý: Khi miền V có dạng hình cầu, hàm dưới dấu tích phân chứa các biểu thức dạng \( {{x}^{2}}+{{y}^{2}} \) hoặc \( {{x}^{2}}+{{y}^{2}}+{{z}^{2}} \) nên chuyển sang tọa độ cầu hoặc tọa độ trụ để tính toán cho đơn giản hơn. Ta có thể kiểm tra lại kết quả của ví dụ trên bằng cách dùng tọa độ trụ.
Trong quá trình đăng tải bài viết lên website không thể tránh khỏi việc sai sót, nên bạn đọc muốn xem đầy đủ các dạng bài tập giải chi tiết hãy vui lòng mua sách Giải bài tập Giải Tích 2!
