Bài Giảng Toán Cao Cấp
2.4.1. Công thức tính tích phân bội ba trong hệ tọa độ Descartes
Định lí 2.3: Nếu \( f(x,y,z) \) liên tục trong miền V cho bởi hệ bất phương trình:
\( \left\{ \begin{align} & a\le x\le b \\ & {{y}_{1}}(x)\le y\le {{y}_{2}}(x) \\ & {{z}_{1}}(x,y)\le y\le {{z}_{2}}(x,y) \\ \end{align} \right.\,\,\,\,\,\,\,\,\,\,\,\,(2.18) \) thì \( \iiint\limits_{V}{f(x,y,z)dxdydz}=\int\limits_{a}^{b}{dx}\int\limits_{{{y}_{1}}(x)}^{{{y}_{2}}(x)}{dy}\int\limits_{{{z}_{1}}(x,y)}^{{{z}_{2}}(x,y)}{f(x,y,z)dz}\,\,\,\,\,\,\,\,\,\,\,\,(2.19) \)
Hệ bất phương trình (2.18) mô tả miền V là một hình trụ cong giới hạn phía trên bởi mặt \( z={{z}_{2}}(x,y) \), giới hạn phía dưới bợi mặt \( z={{z}_{1}}(x,y) \) và giới hạn xung quanh bởi mặt trụ có đường sinh song song với trục Ox, đường chuẩn là biên của miền D (miền Dxy là hình chiếu của V trên mặt phẳng Oxy (H.2.12)), cụ thể miền D cho bởi hệ bất phương trình: \( \left\{ \begin{align} & a\le x\le b \\ & {{y}_{1}}(x)\le y\le {{y}_{2}}(x) \\ \end{align} \right. \).
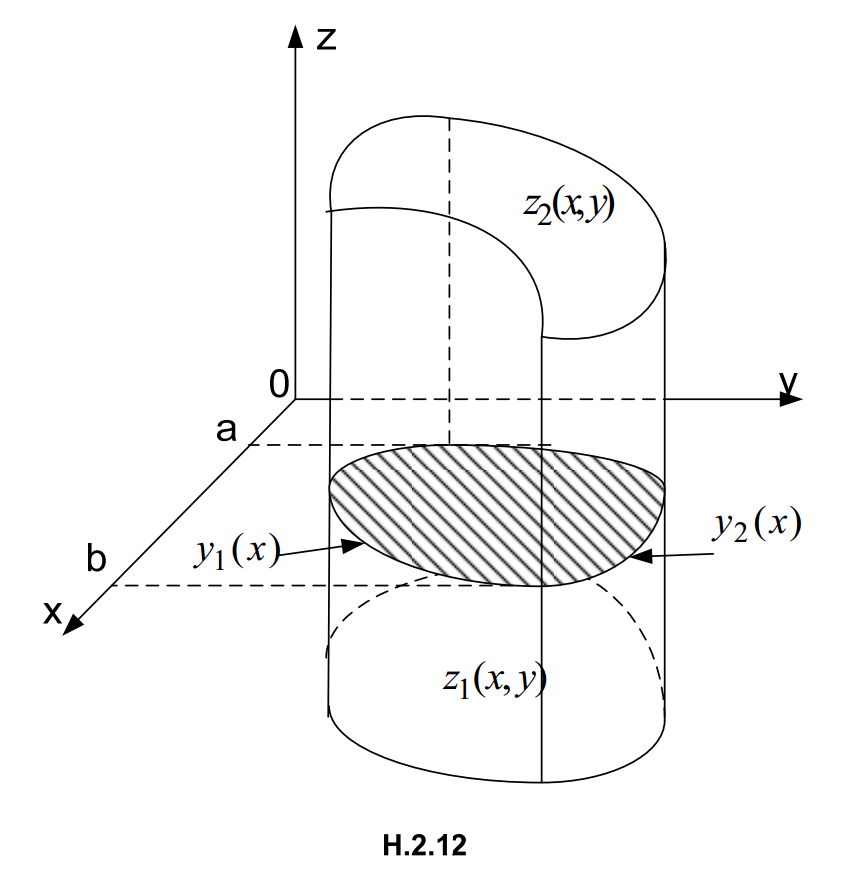
Công thức (2.19) chứng tỏ để tính tích phân bội ba ta đưa về tính tích phân lặp. Khi tính tích phân theo biến z ta coi x, y là hằng số. Khi tính tích phân theo biến y coi x là hằng số. Cuối cùng tính tích phân theo biến x.
Nhận Dạy Kèm môn Giải Tích 2 - Calculus II Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Toán Cao Cấp gồm:
- Giải Tích 1, Giải Tích 2, Giải tích 3
- Đại Số Tuyến Tính, Xác Suất Thống Kê
- Sách Giải Bài Tập của bộ môn Toán Cao Cấp!
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học 1,5h - 2h/1 buổi!
+ Chú ý:
a) Từ công thức (2.10) suy ra công thức (2.19) có thể viết lại như sau:
\( \iiint\limits_{V}{f(x,y,z)dxdydz}=\iint\limits_{{{D}_{xy}}}{dxdy}\int\limits_{{{z}_{1}}(x,y)}^{{{z}_{2}}(x,y)}{f(x,y,z)dz}\,\,\,\,\,\,\,\,\,\,\,\,(2.19′) \)
b) Thay đổi vai tròn của các biến x, y z ta cũng có công thức thay đổi thứ tự lấy tích phân bội ba:
\( \iint\limits_{{{D}_{xy}}}{dxdy}\int\limits_{{{z}_{1}}(x,y)}^{{{z}_{2}}(x,y)}{f(x,y,z)dz}=\iint\limits_{{{D}_{yz}}}{dydz}\int\limits_{{{x}_{1}}(y,z)}^{{{x}_{2}}(y,z)}{f(x,y,z)dx}\,\,\,\,\,\,\,\,\,\,\,\,\,(2.19)” \)
Trong đó \( {{D}_{yz}} \) là hình chiếu của miền V lên mặt phẳng \( Oyz \), còn \( x={{x}_{1}}(y,z)x={{x}_{2}}(y,x) \) là các mặt cong dưới và trên theo hướng Oy để tạo ra miền V.
Tương tự: \( \iint\limits_{{{D}_{xy}}}{dxdy}\int\limits_{{{z}_{1}}(x,y)}^{{{z}_{2}}(x,y)}{f(x,y,z)dz}=\iint\limits_{{{D}_{zx}}}{dzdx}\int\limits_{{{y}_{1}}(x,z)}^{{{y}_{2}}(x,z)}{f(x,y,z)dy}\,\,\,\,\,\,\,\,\,\,\,(2.19)”’ \).
Ví dụ 1. Tính \( I=\iiint\limits_{V}{\frac{dxdydz}{{{(1+x+y+z)}^{3}}}} \) trong đó miền V được cho giới hạn bởi các mặt phẳng \( x=0,\,\,y=0,\,\,z=0,\,\,x+y=1,\,\,x+y-z=0 \).
Hướng dẫn giải:
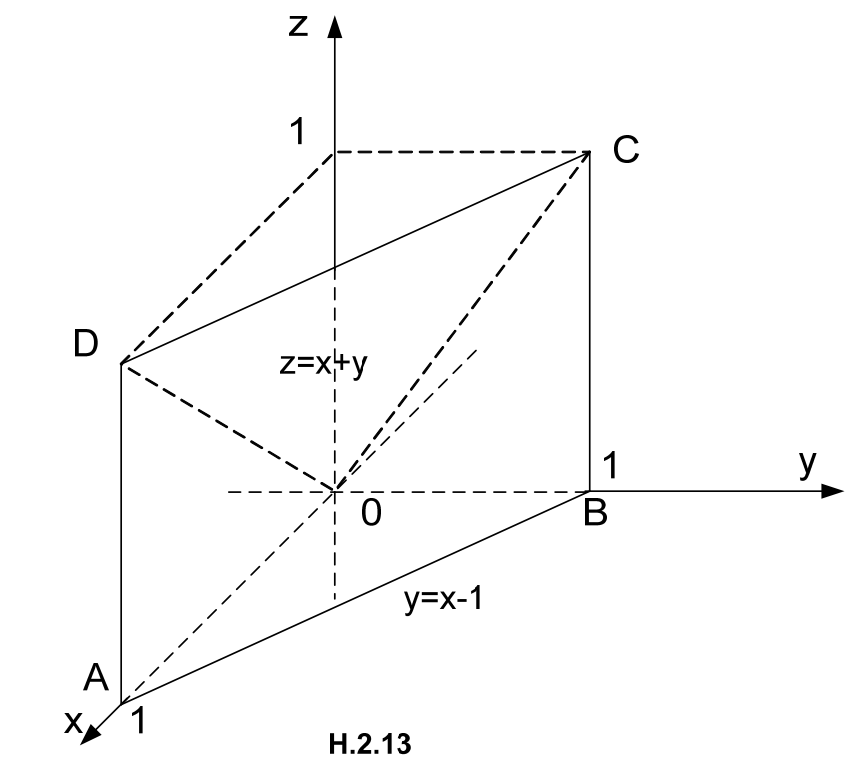
Vẽ miền V (H.2.13). V là hình chóp tứ giác có đỉnh là gốc tọa độ, đáy là hình chữ nhật ABCD. Mặt trên của V (tam giác OCD) là mặt phẳng có phương trình \( z=x+y \). Mặt dưới của V (tam giác OAB) là mặt phẳng có phương trình z=0.
Chiếu V lên mặt phẳng Oxy được tam giác OAB cho bởi hệ bất phương trình: \( \left\{ \begin{align} & 0\le x\le 1 \\ & 0\le y\le 1-x \\ \end{align} \right. \).
Từ đó theo công thức (2.19) có:
\(I=\int\limits_{0}^{1}{dx}\int\limits_{0}^{1-x}{dy}\int\limits_{0}^{x+y}{\frac{1}{{{(1+x+y+z)}^{3}}}dz}=-\frac{1}{2}\int\limits_{0}^{1}{dx}\int\limits_{0}^{1-x}{\left. \frac{1}{{{(1+x+y+z)}^{2}}} \right|_{0}^{x+y}dy}\)
\( =-\frac{1}{2}\int\limits_{0}^{1}{dx}\int\limits_{0}^{1-x}{\left[ \frac{1}{{{(1+2x+2y)}^{2}}}-\frac{1}{{{(2+x+y)}^{2}}} \right]dy}=\frac{1}{2}\int\limits_{0}^{1}{\left. \left( \frac{1}{2(1+2x+2y)}-\frac{1}{1+x+y} \right) \right|_{0}^{1-x}dx} \)
\( =\frac{1}{4}\int\limits_{0}^{1}{\left( \frac{1}{3}-\frac{1}{1+2x} \right)dx}-\frac{1}{2}\int\limits_{0}^{1}{\left( \frac{1}{2}-\frac{1}{1+x} \right)dx}=-\frac{1}{6}-\frac{1}{8}\left. \ln \left| 1+2x \right| \right|_{0}^{1}+\frac{1}{2}\left. \ln \left| 1+x \right| \right|_{0}^{1}=\frac{1}{2}\left( \ln 2-\frac{1}{4}\ln 3-\frac{1}{3} \right) \).
Sách Giải Bài Tập Giải Tích 2
Ví dụ 2. Tính \( I=\iiint\limits_{V}{xdxdydz} \) với V cho bởi hệ bất phương trình: \( \left\{ \begin{align} & x\ge 0 \\ & y\ge 0 \\ & {{x}^{2}}+{{y}^{2}}\le z\le 4 \\ \end{align} \right. \).
Hướng dẫn giải:
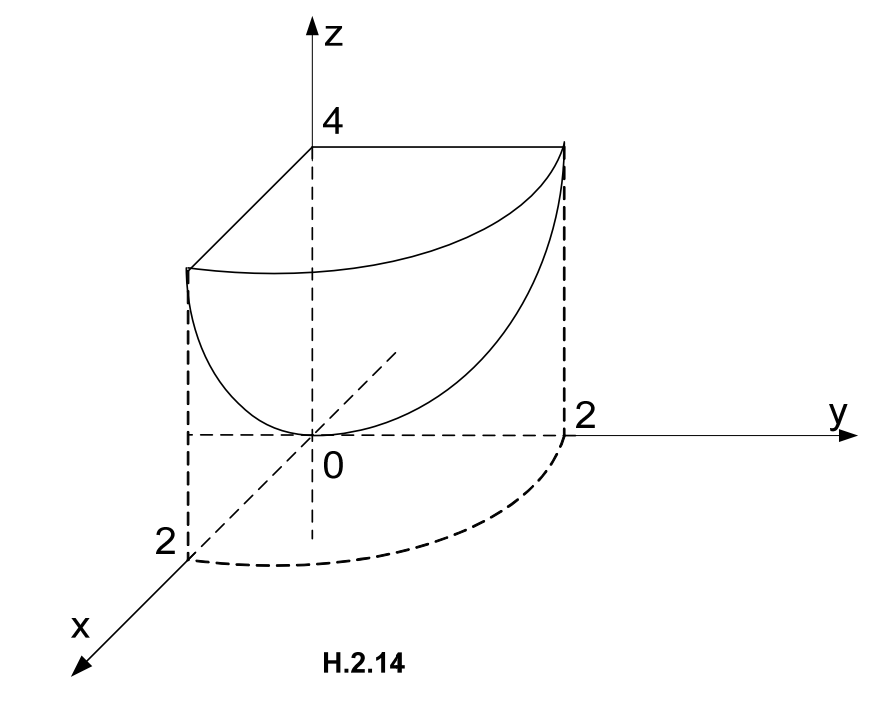
Miền V cho bởi H.2.14. Ta thấy mặt trên của V là \( z=4 \), mặt dưới là paraboloid tròn xoay \( z={{x}^{2}}+{{y}^{2}} \). Hình chiếu D của V lên mặt Oxy là phần tư hình tròn: \( \left\{ \begin{align} & 0\le x\le 2 \\ & 0\le y\le \sqrt{4-{{x}^{2}}} \\ \end{align} \right. \).
Do đó: \( I=\iint\limits_{D}{dxdy}\int\limits_{{{x}^{2}}+{{y}^{2}}}^{4}{xdz}=\iint\limits_{D}{x(4-{{x}^{2}}-{{y}^{2}})dxdy}=\int\limits_{0}^{2}{dx}\int\limits_{0}^{\sqrt{4-{{x}^{2}}}}{x(4-{{x}^{2}}-{{y}^{2}})dy} \)
\( =\int\limits_{0}^{2}{x(4-{{x}^{2}})\sqrt{4-{{x}^{2}}}dx}-\int\limits_{0}^{2}{\frac{x}{3}\cdot \left. {{y}^{3}} \right|_{y=0}^{y=\sqrt{4-{{x}^{2}}}}dx}=-\frac{1}{3}\int\limits_{0}^{2}{{{(4-{{x}^{2}})}^{3/2}}d(4-{{x}^{2}})}=-\frac{1}{3}\cdot \left. \frac{2}{5}{{(4-{{x}^{2}})}^{5/2}} \right|_{0}^{2}=\frac{64}{15} \).
Tương tự như tích phân kép, ta cũng có công thức đổi biến số trong tích phân bội ba dưới đây.
Định lí 2.4: Cho hàm \( f(x,y,z) \) liên tục trên miền \( V\subset Oxyz \) đồng thời tồn tại các hàm số:
\( \left\{ \begin{align} & x=x(u,v,w) \\ & y=y(u,v,w) \\ & z=z(u,v,w) \\ \end{align} \right.,\,\,\,\,(u,v,w)\in \Omega \)
thỏa mãn các điều kiện:
– là song ánh từ V lên \( \Omega \) .
– có các đạo hàm riêng liên tục trong miền \( \Omega \subset Ouvw \) và định thức Jacobi \( \frac{D(x,y,z)}{D(Iu,v,w)}\ne 0 \) trong miền \( \Omega \) (hoặc chỉ bằng 0 ở một số điểm cô lập).
Khi đó: \( \iiint\limits_{V}{f(x,y,z)dxdydz}=\iiint\limits_{\Omega }{f\left[ x(u,v,w),y(u,v,w),z(u,v,w) \right]\cdot \left| \frac{D(x,y,z)}{u,v,w} \right|dudvdw}\,\,\,\,\,\,\,\,\,(2.20) \)
Trong quá trình đăng tải bài viết lên website không thể tránh khỏi việc sai sót, nên bạn đọc muốn xem đầy đủ các dạng bài tập giải chi tiết hãy vui lòng mua sách Giải bài tập Giải Tích 2!
Các bài viết cùng chủ đề!
Các Sách Giải Bài Tập - Đề Thi do Trung tâm phát hành!
Bài Giảng Toán Cao Cấp được xây dựng trên WordPress
